June 16, 2023

Computer vision by deeplearning

The Lottery Tickets Hypothesis for Supervised Pre-training in depth estimation models.

Abstract

Abstract: In the field of computer vision, pre-trained models have gained renewed attention, including ImageNet supervised pre-training. Recent studies have highlighted the enduring significance of the Lottery Tickets Hypothesis (LTH) in the context of classification, detection, and segmentation tasks. Inspired by this, we set out to explore the potential of LTH in the pre-training paradigm of depth estimation. Our aim is to investigate whether we can significantly reduce the complexity of pre-trained models without compromising their downstream transferability in the depth estimation task. We fine-tune the sparse pre-trained networks obtained through iterative magnitude pruning and demonstrate universal transferability to the depth estimation task, maintaining performance comparable to that of fine tuning on the full pre-trained model. Our findings are inconclusive.

Introduction

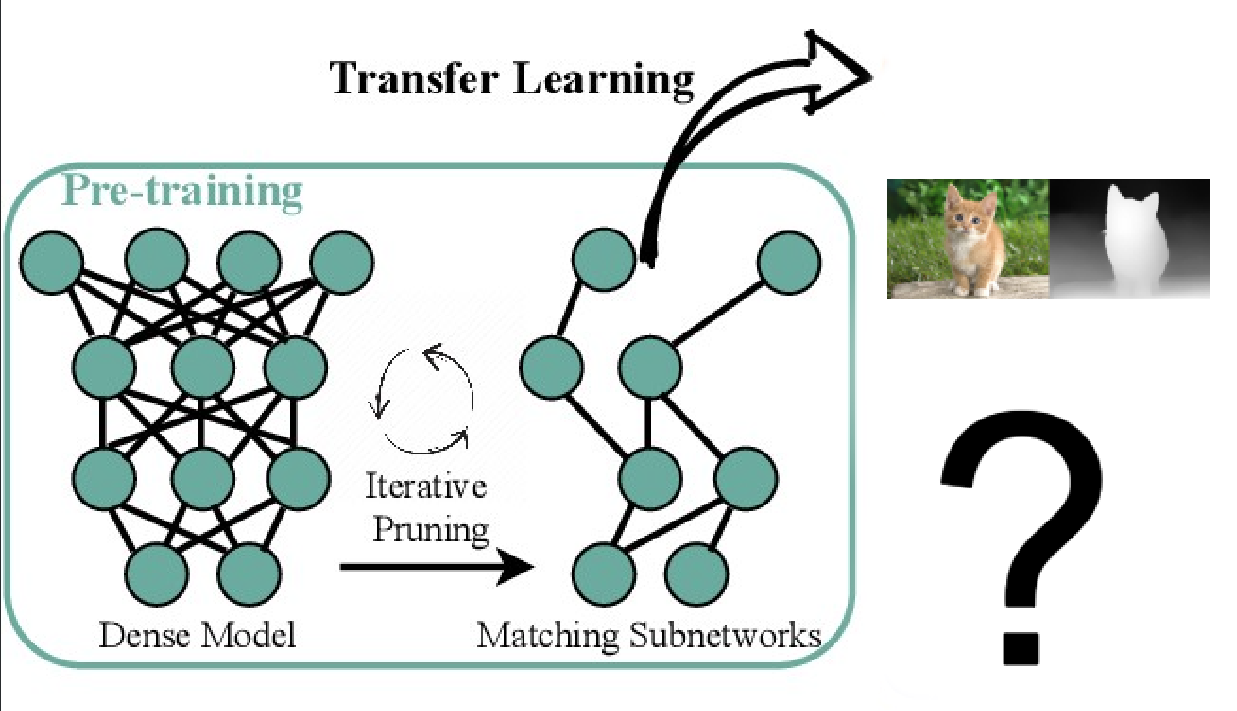
In the realm of computer vision, the resurgence of interest in pre-trained models, including classical ImageNet supervised pre-training, has sparked enthusiasm. Recent studies suggest that the core observations of the Lottery Tickets Hypothesis (LTH) remain relevant in the pre-training paradigm of classification, detection, and segmentation tasks (Chen et al., 2021) as displayed in the following figure.

Description of the image — Studies show that within pre-trained computer vision models (both supervised and self-supervised), there are matching subnetworks that exhibit transferability to multiple downstream tasks, with minimal performance degradation compared to using the full pre-trained weights. Task-agnostic and universally transferable subnetworks are found during pre-trained initialization, benefiting classification, detection, and segmentation tasks.(Chen et al., 2021)

Driven by curiosity, we pose the following question:

Can we aggressively trim down the complexity of pre-trained models without compromising their downstream transferability on the depth estimation task?

In this engaging blog post, we explore the concept of supervised pre-trained models through the lens of the Lottery Tickets Hypothesis (LTH) (Frankle & Carbin, 2019). LTH identifies highly sparse matching subnetworks that can be trained almost from scratch and still achieve comparable performance to the full models. Extending the scope of LTH, we investigate whether such matching subnetworks exist in pre-trained computer vision models, specifically examining their transfer performance in the context of depth estimation. Our experiments did not confirm nor deny the possibility of the hypothesis as the experiments failed. The codes and pre-trained models used in our experiments can be accessed on GitHub: github.com/HAJEKEL/CV_LTH_pre-training_depth-estimation. Join us on this fascinating journey as we uncover the untapped potential of pre-trained models and shed light on the intriguing relationship between the Lottery Tickets Hypothesis and depth estimation in computer vision.

Literature research

Lottery ticket hypothesis

During his PhD research, Jonathan Frankle conducted a thorough investigation into the lottery ticket hypothesis. Initially, the hypothesis proposed that it was feasible to identify sparse subnetworks within dense networks that would perform comparably to the dense network after training. This approach relied on iterative magnitude pruning, where the network was trained until convergence. Subsequently, all weights below a certain magnitude threshold were pruned, and the remaining weights were reset to their initial random values. This process was repeated until the desired sparsity level was achieved, while still preserving the performance of the dense model as displayed in the following gif.

However, it was later revealed that this hypothesis did not hold for larger models. As a result, Frankle put forth a modified hypothesis that was applicable to larger models. Instead of resetting the weights to their original random initialization, he proposed resetting them to an earlier point in the training process. This breakthrough led to the publication of the influential paper "Linear Mode Connectivity and the Lottery Ticket Hypothesis," which demonstrated that regardless of the stochastic gradient descent (SGD) noise, models would converge to the same linearly connected minimum when initialized at an early training point instead of their random initialization as displayed in the following image.

Building upon these seminal findings, our study focuses on applying this second approach in the context of a large ResNet-50 model trained on ImageNet. We employ iterative magnitude pruning, where the remaining weights are iteratively reset to an early point in training. Specifically, we investigate the application of this resetting method in iterative magnitude pruning for pre-trained classification models on ImageNet. Furthermore, we utilize the obtained weight mask to validate that the downstream transferability for monocular depth estimation is not compromised. Depth estimation is a crucial step towards inferring scene geometry from 2D images. The goal in monocular depth estimation is to predict the depth value of each pixel or inferring depth information, given only a single RGB image as input. This is generally done using an encoder decoder network. By delving into the implications of the modified lottery ticket hypothesis and leveraging the iterative magnitude pruning technique on a pre-trained model, our research aims to provide compelling evidence supporting the preservation of downstream transferability in the realm of depth estimation.

Methods

This section descripes the experiments done. First the models used are described after which the exact mask used will be described. The final part of this section describes all specifics about the training procedure.

Model

For the experiments the FCRN model architecture will be used, this model architecture was proposed by Laina et al. (2016), the model uses ResNet-50 as a base and a self-designed upsampling end. Instead of the fully connected end layer,reinforce the relevance of LTH in the pre-training paradigm of depth estimation, paving the way for more efficient and effective depth estimation models. which is used for pre-training, the model has upsampling blocks to generate the 2D depth estimation output.

Masking

As described above, we want to combine the proposed model, with the masking of the lottery hypothesis paper. To do this we mask the model using a mask provided by Chen et al. (2021). The mask used had a sparsity of 1.88%

Dataset

For training the model we used the depth dataset of NYU, it consists of 1449 frames of rgb-Depth pictures. We only use the labeled part of the dataset and not the unlabeled part which is even bigger. For more information about the dataset look at this page: nyu dataset

Training procedure

The models were trained on the labeled section of the NYU depth dataset, we trained till convergence for both the sparse and dense model. For the loss function we took the berHu loss which was used by Laina et al. (2016) and design by (L. Zwald and S. Lambert-Lacroix., 2012).

loss function

For training we created our own pipeline to connect the dataset and the model. The berHu loss function was used to train the model, it is a loss function that combines the L1 and L2 losses based on the highest pixel error in each minibatch (L. Zwald and S. Lambert-Lacroix., 2012). This choice was made because it was used by Laina et al. (2016) on the same task.

optimizer

The standard torch SGD optimizer was used to change the values based on the gradients coming from the loss function. We used a learning rate of 0.0001 for the Resnet-50 part of the model and a learning rate of 0.002 (x20) for the upsampling blocks. The momentum parameter (β) was set to 0.9 and weight decay was set to 0.01. These setting were taken from the code of Laina et al. (2016) except for the learning rate, which originally was 0.001. The learning rate was decreased, because the model would diverge exponentially in the first epochs

As one of the compared models is masked, we need to mask the gradients of this model as well. This is done using the same mask used for masking the model itself.

Results

Below are some depth maps generated by the models, as you can see

To answer our research question : Can we aggressively trim down the complexity of pre-trained models without compromising their downstream transferability on the depth estimation task?, we evaluated multiple criteria presented in previous papers. The values are the relative distance(rel), relative mean squared error (rms) and its log. The final three columns represent the δ₁₂₃ , which are measure that state how much pixels are correctly esitmated for a given error threshold.

Model	rel	rms	δ₁	δ₂	δ₃
FCRN_dense (Laina et al.(2016))	0.127	0.573	0.811	0.953	0.988
FCRN_dense(OURS)	0.325	1.239	0.428	0.740	0.904
FCRN_sparse(OURS)	0.339	1.407	0.406	0.699	0.886

Unfortunately The resutls show that our model does not work as well as the model of Laina et al., for this there are multiple possible reasons.

The model we compare with used not only the label NYU dataset, but also trained on different data, resulting in better generalization.
The training pipe was self designed, this results in the posibillity for bugs. As can be seen in the graph, the difference between our two models is not that big but there is a big difference with regard to the other model.

From the results we can see that the sparse model does not behave alot worse compared to our dense trained network, but due to the big gap in performance compared to the models of others we cannot give a real conclusive answer to the question.

References

Silberman, N., Hoiem, D., Kohli, P., & Fergus, R. (2012). Indoor Segmentation and Support Inference from RGBD Images. In Lecture Notes in Computer Science (pp. 746–760). Springer Science+Business Media. https://doi.org/10.1007/978-3-642-33715-4_54
Laina, I., Rupprecht, C., Belagiannis, V., Tombari, F., & Navab, N. (2016). Deeper Depth Prediction with Fully Convolutional Residual Networks.https://doi.org/10.1109/3dv.2016.32
L. Zwald and S. Lambert-Lacroix. The berhu penalty and the grouped effect. arXiv preprint arXiv:1207.6868, 2012. 2, 4, 5
Frankle, J., & Carbin, M. (2019). The Lottery Tickets Hypothesis for Supervised and Self-supervised Pre-training in Computer Vision Models.
Chen, T., Frankle, J., Chang, S., Liu, S., Zhang, Y., Carbin, M., & Wang, Z. (2021). The Lottery Tickets Hypothesis for Supervised and Self-supervised Pre-training in Computer Vision Models.

Design: HTML5 UP

Computer vision by deeplearning

The Lottery Tickets Hypothesis for Supervised Pre-training in depth estimation models.

Keep reading to learn more

The Lottery Tickets Hypothesis for Supervised Pre-training in depth estimation models.

Abstract

Introduction

Can we aggressively trim down the complexity of pre-trained models without compromising their downstream transferability on the depth estimation task?

Literature research

Lottery ticket hypothesis

Methods

Model

Masking

Dataset

Training procedure

loss function

optimizer

Results

References